Notes on circuit fundamentals
Electricity is one of those fields which seems like a miracle, yet beneath the surface there are rules governing its behavior, just as with any other phenomenon in nature, today I will make a review of some of the rules necessary to work with circuits made of passive components.
The first thing we must do is defining some terms, lets start with the most basic ones in this field.
Current
To put it in simple words electric current is defined as the amount of charge ($Q$) during a period of time $\Delta t$
$$ I_{ave} = \frac{\Delta Q}{\Delta t} $$
If you want to get the instantaneous current just make $\Delta t = 0$:
$$ I = \lim_{\Delta t = 0} \frac{\Delta Q}{\Delta t} = \frac{d Q}{d t} $$
Voltage
In contrast to current there is the voltage, which can be interpreted as “electrical pressure”, its formula is given by: $$ V_{AB} = \frac{\Delta U}{Q} = \frac{U_A - U_B}{Q} = V_A - V_B $$
Ohm’s Law
Because there is not current without a voltage there is a relationship between both phenomenons. This relationship is described by three fundamental elements on every circuit:
- Resistors
- Capacitors
- Inductors
Also known as passive elements, they don’t supply energy, instead they store, dissipate or absorb it.
Resistors
Resistors are known for stopping the current and dissipating its energy as heat. It relates current and Voltage by the following formula:
$$ v(t) = R i(t) \Longleftrightarrow V(s) = R I(s) $$
Capacitors
Capacitors store the energy in form of electric field, it consists of two oppositely charged conducting plates separated by an insulator at a small distance, and they relate current and voltage as follows:
$$ i(t) = C \frac{d v(t)}{dt} \Longleftrightarrow I(s) = s C V(s) $$
$C$ is the capacitance of the device.
Inductors
Like capacitors inductors save energy but this time in terms of magnetic field, the most common form of inductor is a coiled wire. Its behaviour is given by:
$$ v(t) = L \frac{d i(t)}{dt} \Longleftrightarrow V(s) = s L I(s) $$
Laplace Transform
Before continuing let me introduce you the Laplace transform, it is an operation that allow us to convert differential problems in algebraic ones, you might noticed in previous equations the use of variables depending of $t$ and its counterparts using $s$ as the independent variable, well it is the same equation but converted in Laplace terms, It is just a change of perspective, the equations on left side ($t$ equations) can be seen as equations in time domain, while the equations on the right correspond to the same relationships on $frequency$ domain.
Here is the formal definition of the Laplace transform and its inverse:
$$ \mathscr{L} \lbrace f(t) \rbrace = F(s) = \int_0^{\infty} f(t) e^{-st} dt $$
$$ \mathscr{L^{-1}} \lbrace F(s) \rbrace = f(t) = \frac{1}{2 j \pi} \int_{\sigma - j\infty}^{\sigma + j\infty} f(t) e^{st} dt $$
$$ s = \sigma + j\omega $$
At first looks intimidating but it is a great mathematical tool which simplifies the analysis of RLC circuits.
Kirchhoff Laws
The following rules are pretty useful to make an analysis of circuits, with them we can solve any linear circuit:
Kirchhoff Voltage Law (KVL)
The law states that the sums of voltages in a loop will always be equal to 0, it derives from the conservation energy principle:
$$\sum v = 0$$
Current Voltage Law (KCL)
This one is also a simple principle which states that the sum of all currents entering and exiting a node must be equal to 0:
$$\sum i = 0$$
Put it in practice (Filtering)
One the main applications of RLC circuits are filters more specifically frequency filters, here is one example.
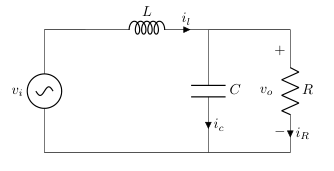
We will find $v_o$ in terms of $v_i$. First lets us Kirchhoff laws:
$$ -v_i + v_L + v_o = 0 $$ $$ v_o = v_i - v_L $$
we don’t need $v_L$, so lets use Ohms Law for an inductor device:
$$ v_L = L \frac{d}{dt} i_L $$
The next step is again use Kirchhoff current law to rewrite $i_L$ in terms of the other device currents, remember sum of input and output currents in a node must be equal to 0, in this case $i_C$ and $i_R$ are output currents while $i_L$, an input one:
$$ i_L = i_C + i_R $$
If we apply again Ohms Law in $i_C$ and $i_L$ we get the following:
$$ i_C = C \dot v_o $$ $$ i_R = \frac{v_o}{R} $$ $$ i_L = C \dot v_o + \frac{v_o}{R} $$
Now we have $i_L$ in terms of $v_o$, we’re close, lets go back to replace $v_L$:
$$ v_L = L \frac{d}{dt} \overbrace{\left( C \dot v_o + \frac{v_o}{R} \right)}^{i_L} $$
$$ v_L = L C \ddot v_o + \frac{L}{R} \dot{v_o} $$
And finally replacing $v_L$ in the first equation allows us to have a relation between $v_i$ and $v_o$:
$$ v_o = v_i - \overbrace{\left( L C \ddot v_o + \frac{L}{R} \dot{v_o} \right)}^{v_L} $$
$$ v_o = v_i - L C \ddot v_o - \frac{L}{R} \dot{v_o} $$
$$ L C \ddot v_o + \frac{L}{R} \dot{v_o} + v_o = v_i $$
Now we got an equation relating $v_i$ and $v_o$, but there is a problem, how do we we actually solve it?, well here is where Laplace transform comes to rescue, the only thing you have to know is that $\mathscr{L}\lbrace\dot{f}(t)\rbrace = s F(s)$, lets apply the transformation to our differential equation:
$$ LC s^2 V_o + \frac{L}{R} s V_o + V_o = V_i $$
We passed from a differential problem to an algebraic one, Lets write $V_o$ in terms of $V_i$:
$$ s^2 V_o + \frac{1}{RC} s V_o + \frac{1}{LC} V_o = \frac{1}{LC} V_i $$
$$ \left( s^2 + \frac{1}{RC} s + \frac{1}{LC} \right) V_o= \frac{1}{LC} V_i $$
$$ V_o = \frac{\frac{1}{LC}}{ s^2 + \frac{1}{RC} s + \frac{1}{LC}} V_i $$
Great! We have the equation, Now what? Well the denominator is a second order polynomial, what about applying the quadratic formula to factorize it:
$$ s = \frac{1}{2} \left( - \frac{1}{RC} \pm \sqrt{\frac{1}{R²C²} - 4 \frac{1}{LC}} \right) $$
Here the analysis become interesting, lets focus on the discriminant:
$$ \frac{1}{R²C²} - 4 \frac{1}{LC} $$
Wether the discriminant is positive or negative, we will get real or complex factors in the denominator, how does this condition affects the behaviour of the circuit? To get an answer suppose $L$ and $C$ are fixed, (it is usual in practical applications), and R can be changed by us and lets rewrite R in terms of $LC$, assuming we want a positive discriminant.
$$ \frac{1}{R²C²} - 4 \frac{1}{LC} \ge 0 $$ $$ R \le \frac{1}{2}\sqrt{\frac{L}{C}} $$
To finish the job we will fix $L$ and $C$ to $10^{-2}$ and $10^{-4}$ respectively and check (with the help of a simulator) how the circuit reacts at different values of $R$. $$ R \le \frac{1}{2}\sqrt{\frac{10^{-2}}{10^{-4}}} = 5$$
There are three scenarios:
- $R < 5$ (e.g 2)
- $R = 5$
- $R > 5$ (e.g 9)
$v_i$ will be a pulse signal and with the help of a simulator we will get its response in time:
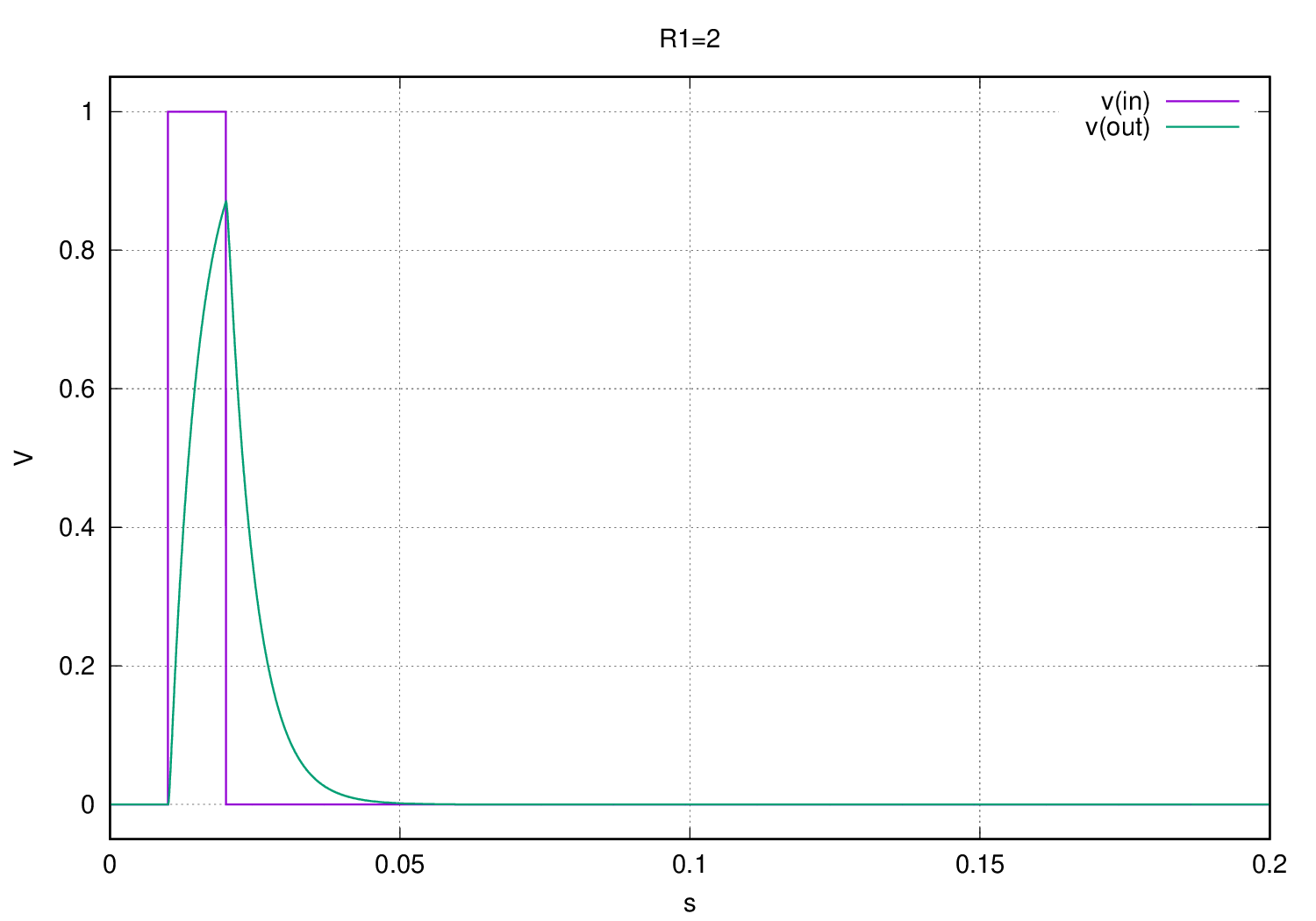
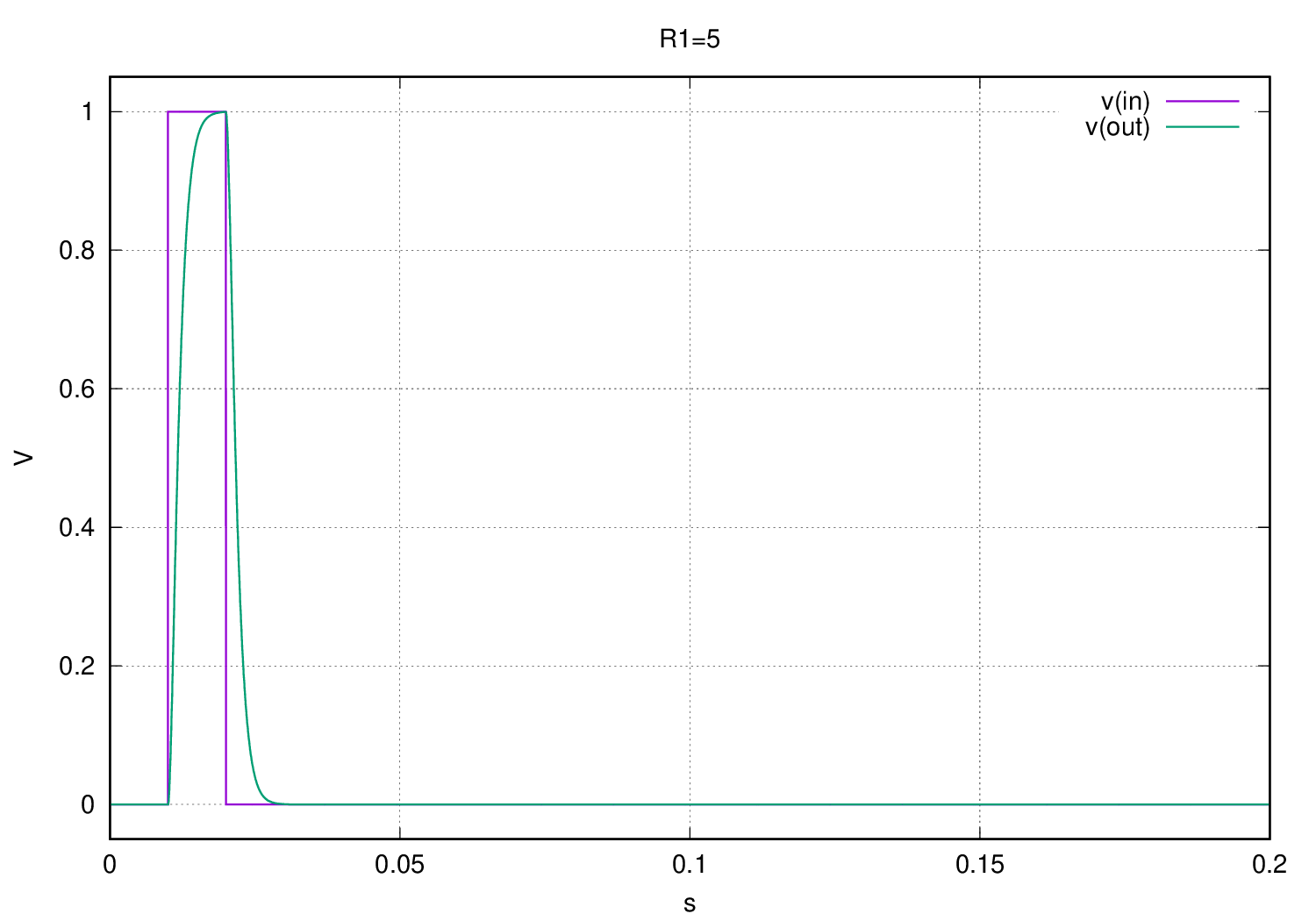
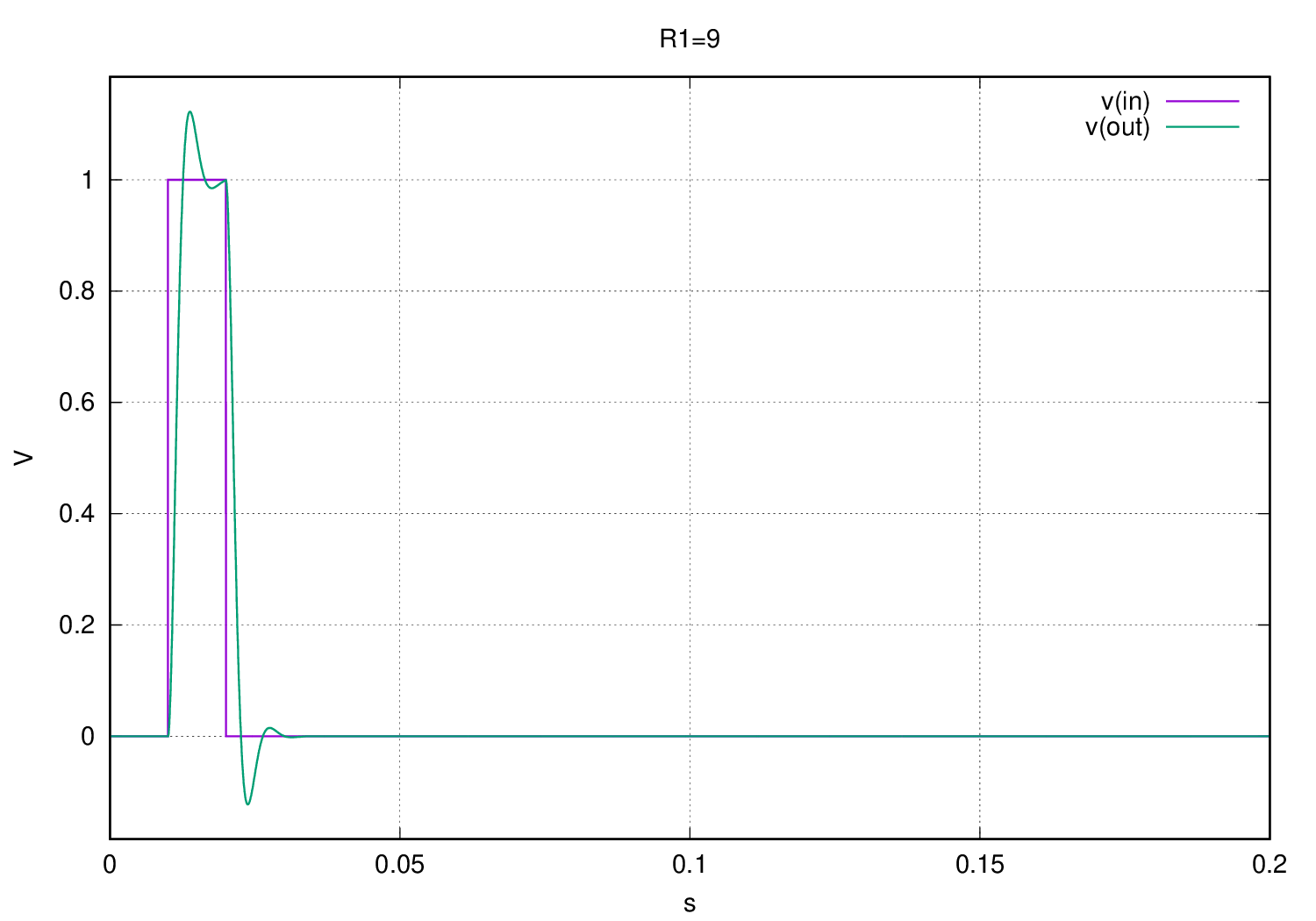
The most evident behaviour is the voltage $v_o$ slow reaction to $v_i$, while $v_i$ has an abrupt changes in the three plots, $v_o$ changes its voltage values at a slower rate, that’s why this circuit is called a low-pass filter, a circuit that filters high frequency variations, we will dive in this later.
The second thing to note is comparing the plots at $R$ equal to $2$ and $5$ against $R=9$ in the third one (where the discriminant is negative), in the third plot $v_o$ oscillates while the others not, why? If we factorize the denominator our circuit equation will have the following form:
$$ V_o = \frac{\frac{1}{LC}}{ s^2 + \frac{1}{RC} s + \frac{1}{LC}} V_i = \frac{\frac{1}{LC}}{(s - f_1)(s - f_2)} V_i $$
$$ V_o = \frac{K_1}{s + f_1} V_i + \frac{K_2}{s + f_2} V_i $$
If you want you can solve $K_1$ and $K_2$ with the fixed values $R$, $C$ and $L$ used previously, but for now pay attention on $f_1$ and $f_2$, these values can be complex (when $R > 5$) or real (when $R \le 5$), and there is an inverse transformation of Laplace that states the following.
$$ \mathscr{L}^{-1}\left\lbrace\frac{1}{s + a}\right\rbrace = e^{at} u(t) $$
In the case $a = \sigma + j\omega_c$ we have that: $$ f(t) = e^{(\sigma + j\omega_c)t} u(t) = e^{\sigma} e^{j \omega_c t} u(t) $$
And: $$e^{j\omega_c} = \cos(\omega_c t) + j \sin (\omega_c t)$$
So having complex factors in the denominator of our circuit equation add sinusoidal components in time domain that will make our circuit to oscillate like the previous example when $R = 9$.
Let’s go back at our first impression of the circuit when we explained why the circuit is called a low-pass filter. We know that our circuit filters high frequencies how much is high?, again we will factorize our equation and this time $V_i$ will be written in the left:
$$ \frac{V_o}{V_i} = \frac{\frac{1}{LC}}{ s^2 + \frac{1}{RC} s + \frac{1}{LC}} = \frac{\frac{1}{LC}}{(s + f_1)(s + f_2)} = H(s) $$
$H(s)$ is known as the transfer function, and it is useful to understand how a circuit will behave at different frequencies. Because $f_1$ and $f_2$ can be complex numbers and therefore $H(s)$ we are interested in getting its Magnitude and phase, the phase tell us how much the output of a circuit delays or advance with respect its input. This analysis can be done using what is called Bode plots, here its definition:
$$ Magnitude = 20 \log{|H(s = j\omega)|} $$
$$ Phase = - \arctan{H(s = j \omega)} $$
Here are Bode plots for the simulations made previously:
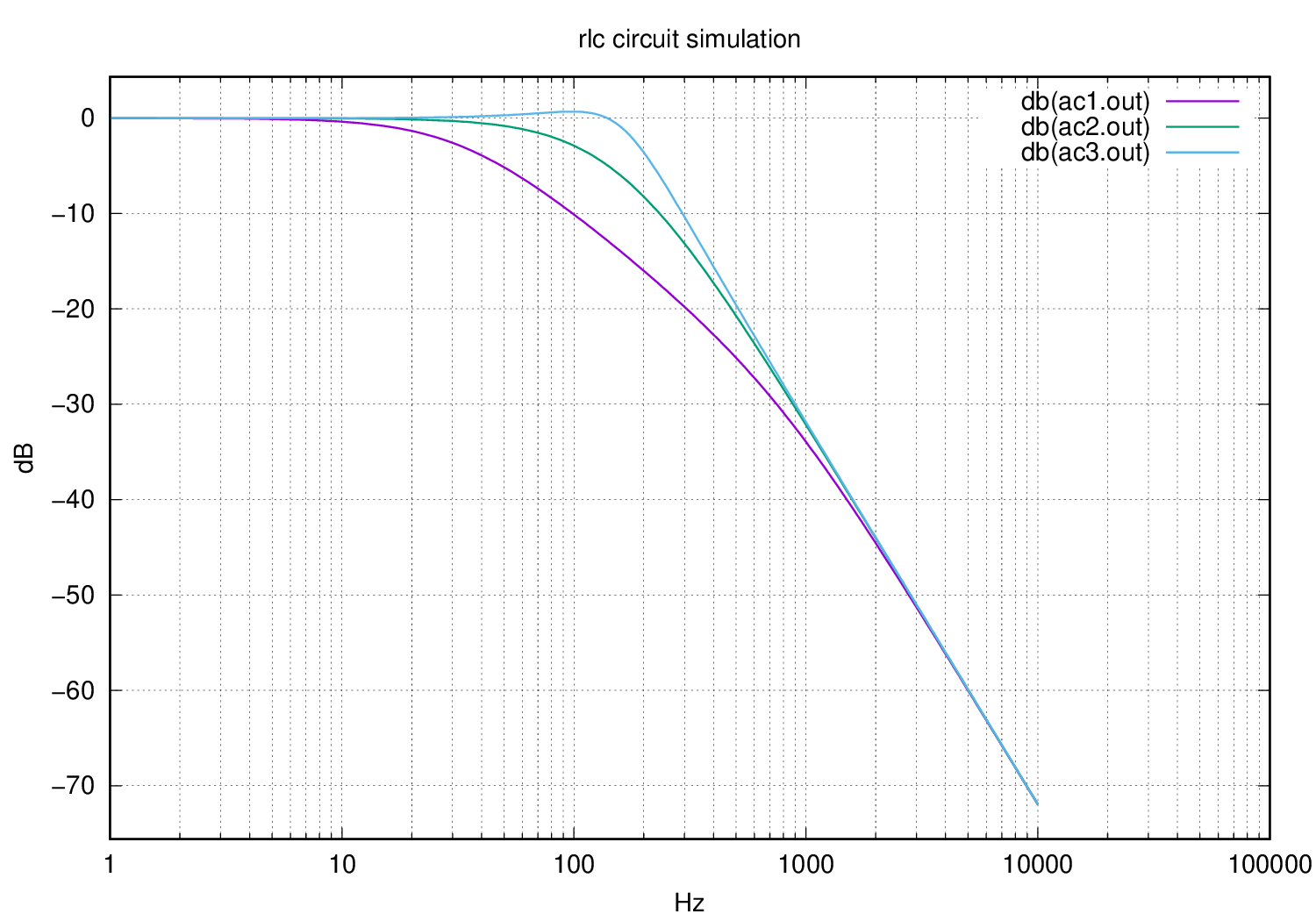
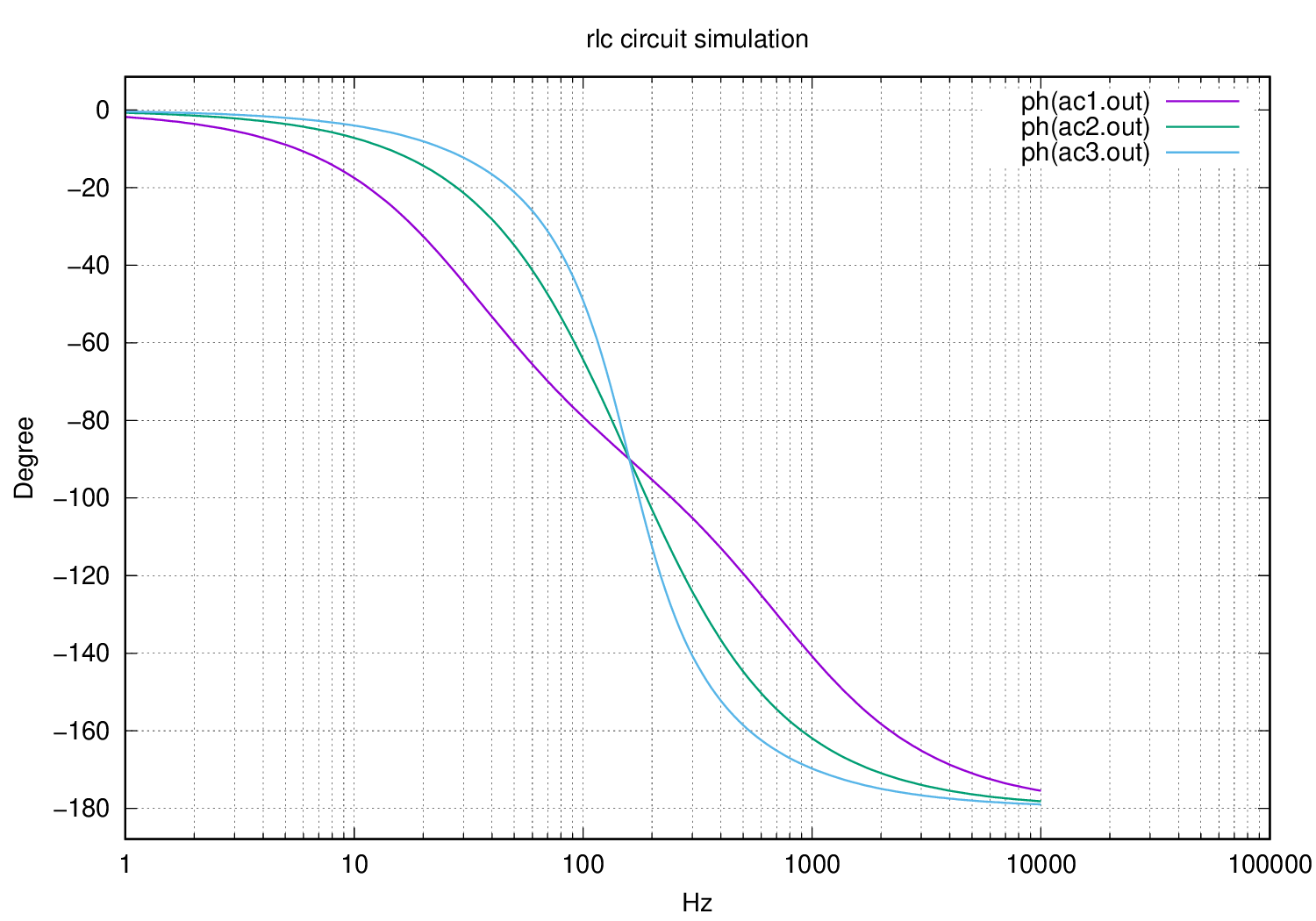
ac1.out, ac2.out, ac3.out correspond to the magnitude and phase plots of the circuit having a resistance $R$ equal to $2$, $5$ and $9$ respectively and x axis is plotted in logarithmic scale due to the asymptotic behaviour of $H(s)$
Every frequency below 3dB is considered as filtered, so here is to the answer to your question, from the plots you can deduce that above certain frequency the signal will only decrease. Now you know which frequencies will be filtered.
In Conclusion
We learnt the fundamental laws of electricity and how to analyze a circuit using the Laplace transform, when it will oscillate and how it will response at certain frequencies.